A key challenge in the embryonic development of complex life forms is the correct specification of cell positions so that organs and limbs grow in the right places. To understand how cells arrange themselves at the earliest stages of development, an interdisciplinary team of applied mathematicians at MIT and experimentalists at Princeton University identified mathematical principles governing the packings of interconnected cell assemblies.
In a paper titled “Entropic effects in cell lineage tree packings,” published this month in Nature Physics, the team reports direct experimental observations and mathematical modeling of cell packings in convex enclosures, a biological packing problem encountered in many complex organisms, including humans.
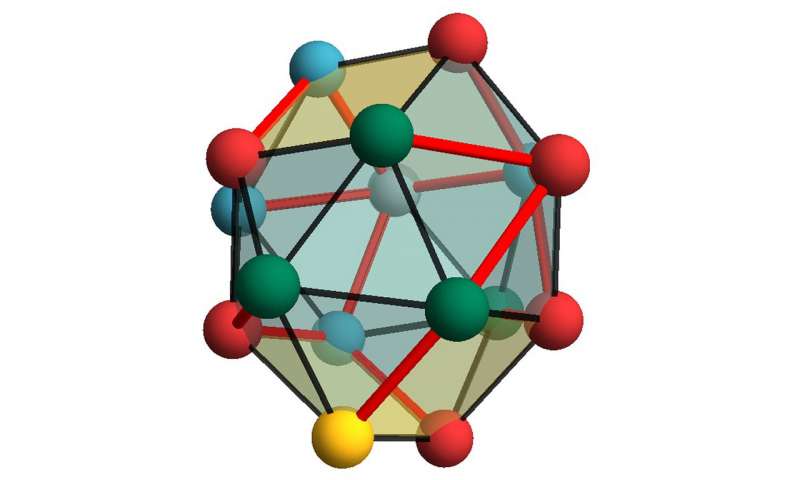
In their study, the authors investigated multi-cellular packings in the egg chambers of the fruit fly Drosophila melanogaster, an important developmental model organism. Each egg chamber contains exactly 16 germline cells that are linked by cytoplasmic bridges, resulting from a series of incomplete cell divisions. The linkages form a branched cell-lineage tree which is enclosed by an approximately spherical hull. At some later stage, one of the 16 cells develops into the fertilizable egg, and the relative positioning of the cells is thought to be important for the biochemical signal exchange during the early stages of development.
The group run by Princeton’s Stanislav Y. Shvartsman, a professor of chemical and biological engineering, and the Lewis-Sigler Institute for Integrative Genomics at Princeton succeeded in measuring the spatial positions and connectivities between individual cells in more than 100 egg chambers. The experimentalists found it difficult to explain, however, why certain tree configurations occurred much more frequently than others, says Jörn Dunkel, an associate professor in the MIT Department of Mathematics.
So while Shvartsman’s team were able to visualize the cell connections in complex biological systems, Dunkel and postdoc Norbert Stoop, a recent MIT math instructor, began to develop a mathematical framework to describe the statistics of the observed cell packings.
Find your dream job in the space industry. Check our Space Job Board »
“This project has been a prime example of an extremely enjoyable interdisciplinary collaboration between cell biology and applied mathematics,” Dunkel says. The experiments were performed by Shvartsman’s Ph.D. student Jasmin Imran Alsous, who will begin a postdoctoral position at Adam Martin’s lab in the MIT Department of Biology this fall. They were analyzed in collaboration with postdoc Paul Villoutreix, who is now at the Weizmann Institute of Science in Israel.
Dunkel points out that while human biology is considerably more complex than a fruit fly’s, the underlying tissue organization processes share many common aspects.
“The cell trees in the egg chamber store the history of the cell divisions, like an ancestry tree in a sense,” he says. “What we were able to do was to map the problem of packing the cell tree into an egg chamber onto a nice and simple mathematical model that basically asks: If you take the fundamental convex polyhedrons with 16 vertices, how many different ways are there to embed 16 cells on them while keeping all the bridges intact?”
The presence of rigid physical connections between cells adds interesting new constraints that make the problem different from the most commonly considered packing problems, such as the question of how to arrange oranges efficiently so that they can be transported in as few containers as possible. The interdisciplinary study of Dunkel and his colleagues, which combined modern biochemical protein labelling techniques, 3-D confocal microscopy, computational image analysis, and mathematical modeling, shows that constrained tree packing problems arise naturally in biological systems.
Understanding the packing principles of cells in tissues at the various stages of development remains a major challenge. Depending on a variety of biological and physical factors, cells originating from a single founder cell can develop in vastly different ways to form muscles, bones, and organs such as the brain. While the developmental process “involves a huge number of degrees of freedom, the end result in many cases is highly complex yet also very reproducible and robust,” Dunkel says.
“This raises the question, which many people asked before, whether such robust complexity can be understood in terms of a basic set of biochemical, physical, and mathematical rules,” he says. “Our study shows that simple physical constraints, like cell-cell bridges arising from incomplete divisions, can significantly affect cell packings. In essence, what we are trying to do is to identify relatively simple tractable models that allow us to make predictions about these complex systems. Of course, to fully understand embryonic development, mathematical simplification must go hand-in-hand with experimental insight from biology.”
Since incomplete cell-divisions have also been seen in amphibians, mollusks, birds, and mammals, Dunkel hopes the modeling approach developed in the paper might be applicable to those systems as well.
“Physical constraints could play a significant role in determining the preferences for certain types of multicellular organizations, and that may have secondary implications for larger-scale tissue dynamics which are not yet clear to us. A simple way you can think about it is that these cytoplasmic bridges, or other physical connections, can help the organism to localize cells into desired positions,” he says. “This would appear to be a very robust strategy.”
Provided by:
Massachusetts Institute of Technology
More information:
Jasmin Imran Alsous et al. Entropic effects in cell lineage tree packings. Nature Physics (2018). DOI: 10.1038/s41567-018-0202-0
Image:
This illustration shows the embedding of a cell lineage tree on a convex equilateral polygon with 16 vertices. Cell connections are shown in red
Credit: Norbert Stoop