A collaboration of a mathematician and a physicist has shown that the modular forms associated with elliptic curves with complex multiplications are expressed in terms of observables in superstring theory.
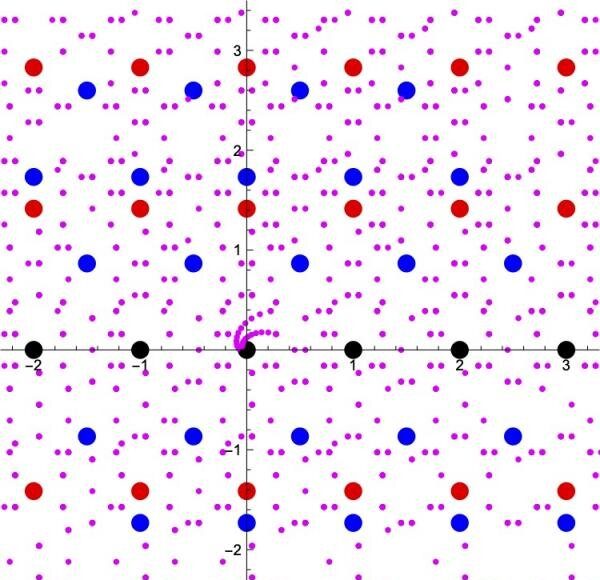
The concept of numbers can be extended from integers and rational numbers to include all real numbers and complex numbers, all at once. But it is also possible to extend the concept gradually, by adding the roots of polynomials with rational number coefficients (such as the square root of 2 and the square root of 3) little by little (Figure 1). This special class of complex numbers are referred to as “numbers.” The precise details of how the concept of numbers can be extended has been considered as one of the important themes in number theory.
For several decades, researchers have tried to address and understand this problem. One could specify a geometric object by equations using the “numbers” first, and then consider the set of points in the geometric object whose values are the “numbers.” As the concept of numbers is gradually extended, and the set of “numbers” expanded, more and more points in the geometric object come to be counted (Figure 2). The idea is that the way the number of points in the geometric object increases will shed light on how the set of “numbers” expands. Furthermore, this information of the growth rate of the number of points in the geometric object is packed into a function called the inverse Mellin transform of the L-function, which is a function containing the information of how fast the number of points in a geometric object grows as the concept of numbers is extended. This function has been expected to be a modular form, a function that remains invariant under certain operations. This conjecture is known as Langlands conjecture.
Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU) Associate Professor and particle theorist Taizan Watari and arithmetic geometry researcher at Middle East Technical University Northern Cyprus Campus and Kavli IPMU Visiting Scientist Satoshi Kondo dared to ask why such functions are invariant under certain operations.
In string theory, it is known that a class of observables (a) are invariant under the operations (x) that have been referred to already. The invariance under the operations is an indispensable property in the theoretical construction of superstring theory. So, the researchers showed that the inverse Mellin transforms of the L-functions of geometry objects (b) are expressed in terms of the above class of observables (a) in superstring theory with those geometric objects set as the target spaces. As a result, it follows that the functions containing the information of how the concept of numbers is extended, the inverse Mellin transforms, (b) should be invariant under certain operations, which should be modular forms, (x) for reasons from the perspective of superstring theory.
Find your dream job in the space industry. Check our Space Job Board »
It should be noted that the result above is obtained only for the class of geometric objects called elliptic curves with complex multiplications. The question remains open to whether the functions for more general class of geometric objects (b) are expressed in terms of observables in superstring theory (a).
Details of this study were published on February 22, 2019, in Communications in Mathematical Physics.
Provided by Kavli Institute for the Physics and Mathematics of the Universe
More information: Satoshi Kondo et al. String-Theory Realization of Modular Forms for Elliptic Curves with Complex Multiplication. Communications in Mathematical Physics (2019). DOI: 10.1007/s00220-019-03302-0
Image: Figure 1. Extension of the concept of integral “numbers”. Black points are the ordinary integers shown in a complex plane. Addition or multiplication of any pair of black points ends up with another black point. All the red points and blue points in this figure are solutions to some quadratic equations with integer coefficients. The purple points are solutions to some quartic equations with integer coefficients. So, we can think of those points also as a part of “numbers”. Addition and multiplication operations among black-or-red points remain within the “numbers” shown in black-or-red points, and similarly, those operations of black-red-blue-or-purple points remain within the “numbers” in black-red-blue-or-purple points. In this way, it is possible to expand the set of integral “numbers” gradually.
Credit: Kavli IPMU