Tiny magnetic whirls that can occur in materials—so-called skyrmions—hold high promises for novel electronic devices or magnetic memory in which they are used as bits to store information. A fundamental prerequisite for any application is the stability of these magnetic whirls. A research team of the Institute of Theoretical Physics and Astrophysics of Kiel University has now demonstrated that so far neglected magnetic interactions can play a key role for skyrmion stability and can drastically enhance skyrmion lifetime. Their work, which has been published today in Nature Communications, opens also the perspective to stabilize skyrmions in new material systems in which the previously considered mechanisms are not sufficient.
Intensive research on stability at room temperature
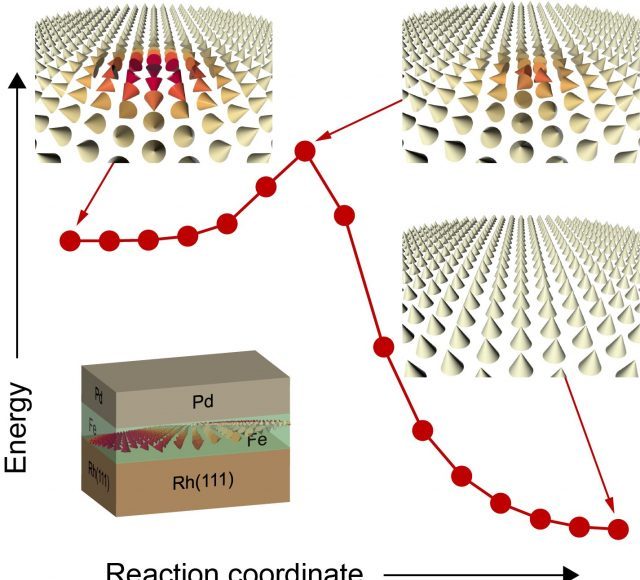
Their unique magnetic structure—more precisely their topology—lends stability to skyrmions and protects them from collapse. Therefore, skyrmions are denoted as knots in the magnetization. However, on the atomic lattice of a solid this protection is imperfect and there is only a finite energy barrier (Figure 1). “The situation is comparable to a marble lying in a trough which thus needs a certain impetus, energy, to escape from it. The larger the energy barrier, the higher is the temperature at which the skyrmion is stable,” explains Professor Stefan Heinze from Kiel University. Especially skyrmions with diameters below 10 nanometers, which are needed for future spinelectronic devices, have so far only been detected at very low temperatures. Since applications are typically at room temperature the enhancement of the energy barrier is a key objective in today’s research on skyrmions.
Previously, a standard model of the relevant magnetic interactions contributing to the barrier has been established. A team of theoretical physicists from the research group of Professor Stefan Heinze has now demonstrated that one type of magnetic interactions has so far been overlooked. In the 1920s Werner Heisenberg could explain the occurrence of ferromagnetism by the quantum mechanical exchange interaction which results from the spin dependent “hopping” of electrons between two atoms. “If one considers the electron hopping between more atoms, higher-order exchange interactions occur,” says Dr. Souvik Paul, first author of the study (Figure 2). However, these interactions are much weaker than the pair-wise exchange proposed by Heisenberg and were thus neglected in the research on skyrmions.
Weak higher-order exchange interactions stabilize skyrmions
Find your dream job in the space industry. Check our Space Job Board »
Based on atomistic simulations and quantum mechanical calculations performed on the super computers of the North-German Supercomputing Alliance (HLRN) the scientists from Kiel have now explained that these weak interactions can still provide a surprisingly large contribution to skyrmion stability. Especially the cyclic hopping over four atomic sites (see red arrows in Fig. 2) influences the energy of the transition state extraordinarily strongly (see Fig. 1 highest point on the upper right), where only a few atomic bar magnets are tilted against each other. Even stable antiskyrmions were found in the simulations which are advantageous for some future data storage concepts but typically decay too fast.
Higher-order exchange interactions appear in many magnetic materials used for potential skyrmion applications such as cobalt or iron. They can also stabilize skyrmions in magnetic structures in which the previously considered magnetic interactions cannot occur or are too small. Therefore, the present study opens new promising routes for the research on these fascinating magnetic knots.
More information: Souvik Paul et al. Role of higher-order exchange interactions for skyrmion stability. Nature Communications (2020). DOI: 10.1038/s41467-020-18473-x
Image: Fig. 1: Stabilization of skyrmions by higher-order exchange interactions. The red curve shows the energy barrier for the collapse of a magnetic skyrmion (upper left) into the ferromagnetic background (lower right). At the highest point of the curve defining the barrier height one finds the transition state (upper right). The cones show the “atomic bar magnets” of individual atoms on a hexagonal lattice. Silver arrows denote cones pointing upwards while red color specifies cones pointing downwards. Lower left: Schematic structure of an atomic layer of palladium (Pd) on an atomic layer of iron (Fe) deposited on a rhodium (Rh) surface with (111) crystallographic orientation.
Credit: Kiel University